Was sind innere und äußere Zäune?

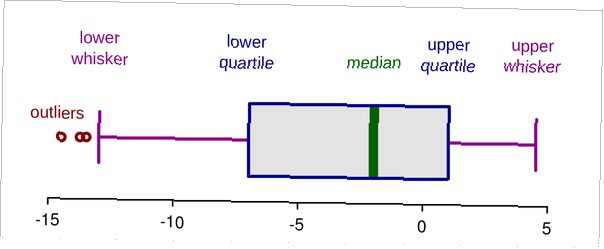
Ein Merkmal eines Datensatzes, das zu bestimmen ist, ist, ob er Ausreißer enthält. Ausreißer werden intuitiv als Werte in unserem Datensatz angesehen, die sich stark von den meisten anderen Daten unterscheiden. Natürlich ist dieses Verständnis von Ausreißern nicht eindeutig. Um als Ausreißer zu gelten, um wie viel sollte der Wert vom Rest der Daten abweichen? Wird das, was ein Forscher einen Ausreißer nennt, mit dem eines anderen übereinstimmen? Um eine gewisse Konsistenz und ein quantitatives Maß für die Ermittlung von Ausreißern zu gewährleisten, verwenden wir Innen- und Außenzäune.

Um den inneren und äußeren Zaun eines Datensatzes zu finden, benötigen wir zunächst einige andere deskriptive Statistiken. Wir werden mit der Berechnung der Quartile beginnen. Dies führt zum Interquartilbereich. Schließlich werden wir mit diesen Berechnungen in der Lage sein, den inneren und den äußeren Zaun zu bestimmen.

Quartile

Das erste und dritte Quartil sind Teil der Fünf-Zahlen-Zusammenfassung eines beliebigen Satzes quantitativer Daten. Wir beginnen damit, den Median oder die Mitte der Daten zu ermitteln, nachdem alle Werte in aufsteigender Reihenfolge aufgeführt sind. Die Werte unter dem Median entsprechen ungefähr der Hälfte der Daten. Wir finden den Median dieser Hälfte des Datensatzes, und dies ist das erste Quartil.

In ähnlicher Weise betrachten wir nun die obere Hälfte des Datensatzes. Wenn wir den Median für diese Hälfte der Daten finden, haben wir das dritte Quartil. Diese Quartile haben ihren Namen von der Tatsache, dass sie den Datensatz in vier gleich große Teile oder Viertel aufteilen. Mit anderen Worten, ungefähr 25% aller Datenwerte sind kleiner als das erste Quartil. In ähnlicher Weise sind ungefähr 75% der Datenwerte kleiner als das dritte Quartil.

Interquartilbereich

Als nächstes müssen wir den Interquartilbereich (IQR) finden. Dies ist einfacher zu berechnen als das erste Quartil q₁ und das dritte Quartil q₃. Alles was wir tun müssen, ist die Differenz dieser beiden Quartile zu nehmen. Dies gibt uns die Formel:

IQR = Q.₃ - Q.₁

Der IQR gibt an, wie verteilt die mittlere Hälfte unseres Datensatzes ist.

Finde die inneren Zäune

Wir können jetzt die inneren Zäune finden. Wir beginnen mit dem IQR und multiplizieren diese Zahl mit 1,5. Diese Zahl subtrahieren wir dann vom ersten Quartil. Wir addieren diese Zahl auch zum dritten Quartil. Diese beiden Zahlen bilden unseren inneren Zaun.

Finde die äußeren Zäune

Für die äußeren Zäune beginnen wir mit dem IQR und multiplizieren diese Zahl mit 3. Dann subtrahieren wir diese Zahl vom ersten Quartil und addieren sie zum dritten Quartil. Diese beiden Zahlen sind unsere äußeren Zäune.

Ausreißer erkennen

Das Erkennen von Ausreißern wird jetzt so einfach wie das Ermitteln, wo die Datenwerte in Bezug auf unsere inneren und äußeren Zäune liegen. Wenn ein einzelner Datenwert extremer ist als einer unserer äußeren Zäune, ist dies ein Ausreißer und wird manchmal als starker Ausreißer bezeichnet. Liegt unser Datenwert zwischen einem entsprechenden inneren und einem äußeren Zaun, so handelt es sich bei diesem Wert um einen vermuteten oder einen milden Ausreißer. Wir werden sehen, wie dies mit dem folgenden Beispiel funktioniert.

Beispiel

Angenommen, wir haben das erste und dritte Quartil unserer Daten berechnet und diese Werte auf 50 bzw. 60 ermittelt. Der Interquartilbereich IQR = 60 - 50 = 10. Als nächstes sehen wir, dass 1,5 x IQR = 15. Dies bedeutet, dass die inneren Zäune bei 50 - 15 = 35 und 60 + 15 = 75 liegen. Dies ist 1,5 x IQR weniger als der erstes Quartil und mehr als das dritte Quartil.

Wir berechnen jetzt 3 x IQR und sehen, dass dies 3 x 10 = 30 ist. Die äußeren Zäune sind 3 x IQR extremer als das erste und dritte Quartil. Dies bedeutet, dass die äußeren Zäune 50 - 30 = 20 und 60 + 30 = 90 sind.

Alle Datenwerte, die kleiner als 20 oder größer als 90 sind, werden als Ausreißer betrachtet. Bei Datenwerten zwischen 29 und 35 oder zwischen 75 und 90 handelt es sich vermutlich um Ausreißer.