Z-Scores Arbeitsblatt

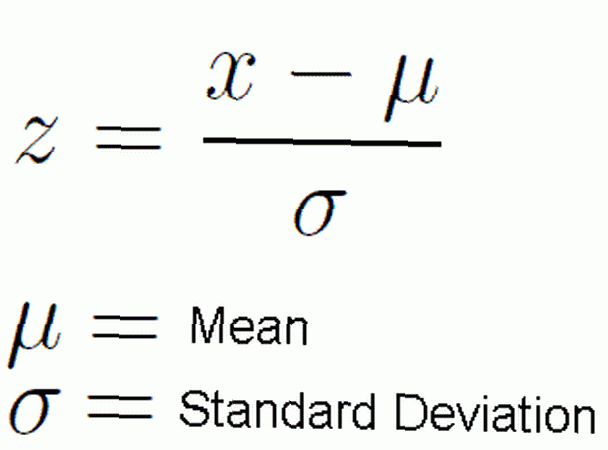
Eine Standardaufgabe aus einem Einführungskurs in die Statistik ist die Berechnung der z-Punktzahl eines bestimmten Wertes. Dies ist eine sehr grundlegende Berechnung, die jedoch sehr wichtig ist. Der Grund dafür ist, dass wir die unendliche Anzahl von Normalverteilungen durchlaufen können. Diese Normalverteilungen können einen Mittelwert oder eine positive Standardabweichung haben.

Das z-Die Bewertungsformel beginnt mit dieser unendlichen Anzahl von Verteilungen und lässt uns nur mit der Standardnormalverteilung arbeiten. Anstatt für jede Anwendung, auf die wir stoßen, mit einer anderen Normalverteilung zu arbeiten, müssen wir nur mit einer speziellen Normalverteilung arbeiten. Die Standardnormalverteilung ist diese gut untersuchte Verteilung.  

Erklärung des Prozesses

Wir gehen davon aus, dass wir in einem Umfeld arbeiten, in dem unsere Daten normal verteilt sind. Wir gehen auch davon aus, dass wir den Mittelwert und die Standardabweichung der Normalverteilung erhalten, mit der wir arbeiten. Mit der Z-Score-Formel: z = (x - μ) / σ können wir jede beliebige Verteilung in die Standardnormalverteilung umrechnen. Hier ist der griechische Buchstabe μ der Mittelwert und σ die Standardabweichung. 

Die Standardnormalverteilung ist eine spezielle Normalverteilung. Es hat einen Mittelwert von 0 und seine Standardabweichung ist gleich 1.

Z-Score Probleme

Alle folgenden Probleme verwenden die Z-Score-Formel. Bei all diesen Übungsproblemen muss anhand der bereitgestellten Informationen ein Z-Score ermittelt werden. Finden Sie heraus, wie Sie diese Formel verwenden können.

1. Die Ergebnisse eines Verlaufstests haben einen Durchschnitt von 80 mit einer Standardabweichung von 6. Was ist das? z-Punktzahl für einen Schüler, der beim Test eine 75 erreicht hat?
2. Das Gewicht von Schokoladenriegeln aus einer bestimmten Schokoladenfabrik beträgt durchschnittlich 8 Unzen mit einer Standardabweichung von 0,1 Unzen. Was ist der z-Punktzahl entsprechend einem Gewicht von 8,17 Unzen?
3. Bücher in der Bibliothek haben eine durchschnittliche Länge von 350 Seiten mit einer Standardabweichung von 100 Seiten. Was ist der z-Punktzahl entsprechend einem Buch mit einer Länge von 80 Seiten?
4. Die Temperatur wird an 60 Flughäfen in einer Region aufgezeichnet. Die durchschnittliche Temperatur beträgt 67 Grad Fahrenheit mit einer Standardabweichung von 5 Grad. Was ist der z-Ergebnis für eine Temperatur von 68 Grad?
5. Eine Gruppe von Freunden vergleicht, was sie während des Süßes oder Saures erhalten haben. Sie stellen fest, dass die durchschnittliche Anzahl der erhaltenen Süßigkeiten 43 beträgt, mit einer Standardabweichung von 2. Was ist das? z-Punktzahl entspricht 20 Stück Süßigkeiten?
6. Das mittlere Wachstum der Baumdicke in einem Wald beträgt 0,5 cm / Jahr mit einer Standardabweichung von 0,1 cm / Jahr. Was ist der z-Punktzahl entspricht 1 cm / Jahr?
7. Ein bestimmter Beinknochen für Dinosaurierfossilien hat eine durchschnittliche Länge von 5 Fuß mit einer Standardabweichung von 3 Zoll. Was ist der z-Punktzahl, die einer Länge von 62 Zoll entspricht?

Überprüfen Sie Ihre Arbeit, sobald Sie diese Probleme behoben haben. Oder vielleicht, wenn Sie nicht weiter wissen, was Sie tun sollen. Lösungen mit einigen Erklärungen finden Sie hier.