Mengenlehre

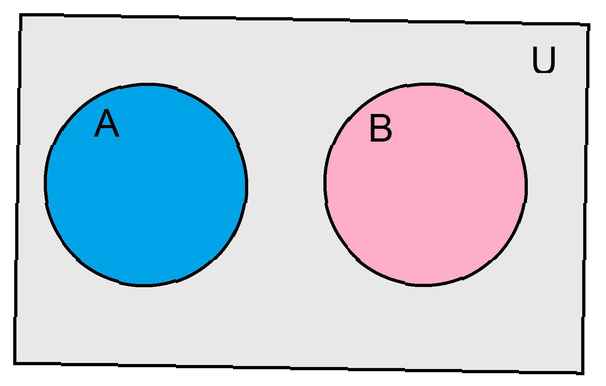
Die Mengenlehre ist ein grundlegendes Konzept in der gesamten Mathematik. Dieser Zweig der Mathematik bildet eine Grundlage für andere Themen. 

Intuitiv ist eine Menge eine Sammlung von Objekten, die als Elemente bezeichnet werden. Obwohl dies eine einfache Idee zu sein scheint, hat es einige weitreichende Konsequenzen. 

Elemente

Die Elemente einer Menge können wirklich alles sein - Zahlen, Zustände, Autos, Menschen oder sogar andere Mengen sind alle Möglichkeiten für Elemente. Fast alles, was zusammen gesammelt werden kann, kann verwendet werden, um ein Set zu bilden, obwohl es einige Dinge gibt, bei denen wir vorsichtig sein müssen.

Gleiche Mengen

Elemente einer Menge befinden sich entweder in einer Menge oder nicht in einer Menge. Wir können eine Menge durch eine definierende Eigenschaft beschreiben oder die Elemente in der Menge auflisten. Die Reihenfolge, in der sie aufgelistet sind, ist nicht wichtig. Die Mengen 1, 2, 3 und 1, 3, 2 sind also gleiche Mengen, da beide die gleichen Elemente enthalten.

Zwei Spezialsets

Zwei Sets verdienen besondere Erwähnung. Der erste ist der universelle Satz, der typischerweise bezeichnet wird U. Dieses Set enthält alle Elemente, aus denen wir auswählen können. Dieser Satz kann sich von einer Einstellung zur nächsten unterscheiden. Beispielsweise kann ein universeller Satz der Satz reeller Zahlen sein, während der universelle Satz für ein anderes Problem die ganzen Zahlen 0, 1, 2,… sein kann.. 

Der andere Satz, der etwas Aufmerksamkeit erfordert, wird als leerer Satz bezeichnet. Die leere Menge ist die eindeutige Menge, die keine Elemente enthält. Wir können dies als schreiben und diese Menge mit dem Symbol ∅ kennzeichnen.

Subsets und das Power Set

Eine Sammlung einiger Elemente eines Sets EIN heißt eine Untermenge von EIN. Wir sagen das EIN ist eine Teilmenge von B genau dann, wenn jedes Element von EIN ist auch ein Element von B. Wenn es eine endliche Zahl gibt n von Elementen in einer Menge, dann gibt es insgesamt 2ⁿ Teilmengen von EIN. Diese Sammlung aller Teilmengen von EIN ist eine Menge, die als Potenzmenge von bezeichnet wird EIN.

Festlegen von Vorgängen

So wie wir Operationen wie Addition ausführen können, um eine neue Zahl zu erhalten, werden Mengenoperationen verwendet, um eine Menge aus zwei anderen Mengen zu bilden. Es gibt eine Reihe von Operationen, aber fast alle setzen sich aus den folgenden drei Operationen zusammen:

• Union - Eine Union bedeutet ein Zusammenbringen. Die Vereinigung der Mengen EIN und B besteht aus den Elementen, die in beiden sind EIN oder B.
• Kreuzung - An einer Kreuzung treffen zwei Dinge aufeinander. Der Schnittpunkt der Mengen EIN und B besteht aus den Elementen, die in beiden EIN und B.
• Komplement - Das Komplement der Menge EIN besteht aus allen Elementen in der universellen Menge, die keine Elemente von sind EIN.

Venn-Diagramme

Ein Werkzeug, das bei der Darstellung der Beziehung zwischen verschiedenen Mengen hilfreich ist, heißt Venn-Diagramm. Ein Rechteck repräsentiert die universelle Menge für unser Problem. Jeder Satz ist mit einem Kreis dargestellt. Überlappen sich die Kreise, so verdeutlicht dies den Schnittpunkt unserer beiden Mengen. 

Anwendungen der Mengenlehre

Die Mengenlehre wird in der gesamten Mathematik verwendet. Es dient als Grundlage für viele Teilgebiete der Mathematik. In den statistischen Bereichen wird es vor allem in der Wahrscheinlichkeitsrechnung eingesetzt. Ein Großteil der Wahrscheinlichkeitsbegriffe leitet sich aus den Konsequenzen der Mengenlehre ab. Ein Weg, um die Axiome der Wahrscheinlichkeit zu formulieren, ist die Mengenlehre.