Standard- und normale Excel-Verteilungsberechnungen
 Share
Share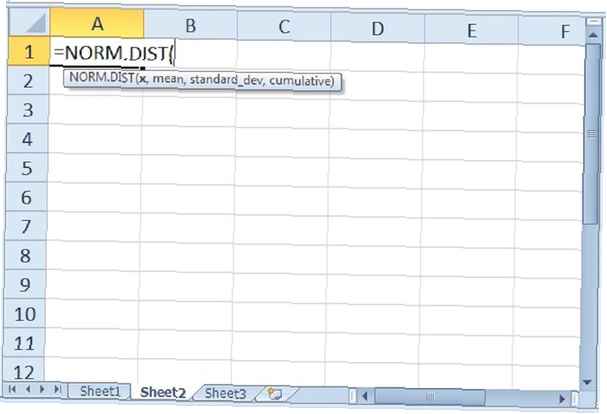
Nahezu jedes statistische Softwarepaket kann für Berechnungen bezüglich einer Normalverteilung verwendet werden, die allgemein als Glockenkurve bekannt ist. Excel ist mit einer Vielzahl statistischer Tabellen und Formeln ausgestattet, und es ist ganz einfach, eine seiner Funktionen für eine Normalverteilung zu verwenden. Wir werden sehen, wie die Funktionen NORM.DIST und NORM.S.DIST in Excel verwendet werden.
Normalverteilungen
Es gibt unendlich viele Normalverteilungen. Eine Normalverteilung wird durch eine bestimmte Funktion definiert, bei der zwei Werte bestimmt wurden: der Mittelwert und die Standardabweichung. Der Mittelwert ist eine beliebige reelle Zahl, die das Zentrum der Verteilung angibt. Die Standardabweichung ist eine positive reelle Zahl, die die Streuung der Verteilung misst. Sobald wir die Werte für Mittelwert und Standardabweichung kennen, ist die jeweilige Normalverteilung, die wir verwenden, vollständig bestimmt.
Die Standardnormalverteilung ist eine Spezialverteilung aus der unendlichen Anzahl von Normalverteilungen. Die Standardnormalverteilung hat einen Mittelwert von 0 und eine Standardabweichung von 1. Jede Normalverteilung kann durch eine einfache Formel auf die Standardnormalverteilung normiert werden. Aus diesem Grund ist in der Regel die einzige Normalverteilung mit angegebenen Werten die der Standardnormalverteilung. Diese Art von Tabelle wird manchmal als Tabelle mit Z-Scores bezeichnet.
NORM.S.DIST
Die erste Excel-Funktion, die wir untersuchen werden, ist die NORM.S.DIST-Funktion. Diese Funktion gibt die Standardnormalverteilung zurück. Für die Funktion sind zwei Argumente erforderlich:z"Und" kumulativ ". Das erste Argument von z ist die Anzahl der Standardabweichungen vom Mittelwert. So, z = -1,5 ist eineinhalb Standardabweichungen unter dem Mittelwert. Das z-Kerbe von z = 2 ist zwei Standardabweichungen über dem Mittelwert.
Das zweite Argument ist das von "kumulativ". Hier können zwei mögliche Werte eingegeben werden: 0 für den Wert der Wahrscheinlichkeitsdichtefunktion und 1 für den Wert der kumulativen Verteilungsfunktion. Um die Fläche unter der Kurve zu bestimmen, möchten wir hier eine 1 eingeben.
Beispiel
Um zu verstehen, wie diese Funktion funktioniert, sehen wir uns ein Beispiel an. Wenn wir auf eine Zelle klicken und = NORM.S.DIST (.25, 1) eingeben, enthält die Zelle nach dem Drücken von enter den Wert 0,5987, der auf vier Dezimalstellen gerundet wurde. Was bedeutet das? Es gibt zwei Interpretationen. Der erste ist, dass die Fläche unter der Kurve für z kleiner oder gleich 0,25 ist 0,5987. Die zweite Interpretation ist, dass 59,87 Prozent der Fläche unter der Kurve für die Standardnormalverteilung auftreten, wenn z ist kleiner oder gleich 0,25.
NORM.DIST
Die zweite Excel-Funktion, die wir uns ansehen werden, ist die NORM.DIST-Funktion. Diese Funktion gibt die Normalverteilung für einen bestimmten Mittelwert und eine bestimmte Standardabweichung zurück. Für die Funktion sind vier Argumente erforderlich:x,"Mittelwert", "Standardabweichung" und "kumulativ". Das erste Argument von x ist der beobachtete Wert unserer Verteilung. Mittelwert und Standardabweichung sind selbsterklärend. Das letzte Argument von "kumulativ" ist identisch mit dem der Funktion NORM.S.DIST.
Beispiel
Um zu verstehen, wie diese Funktion funktioniert, sehen wir uns ein Beispiel an. Wenn wir auf eine Zelle klicken und = NORM.DIST (9, 6, 12, 1) eingeben, enthält die Zelle nach dem Drücken von enter den Wert 0,5987, der auf vier Dezimalstellen gerundet wurde. Was bedeutet das?
Die Werte der Argumente besagen, dass wir mit der Normalverteilung arbeiten, die einen Mittelwert von 6 und eine Standardabweichung von 12 hat. Wir versuchen zu bestimmen, für welchen Prozentsatz der Verteilung auftritt x kleiner oder gleich 9. Entsprechend wollen wir den Bereich unter der Kurve dieser speziellen Normalverteilung und links von der vertikalen Linie x = 9.
NORM.S.DIST vs NORM.DIST
In den obigen Berechnungen sind einige Punkte zu beachten. Wir sehen, dass das Ergebnis für jede dieser Berechnungen identisch war. Dies liegt daran, dass 9 0,25 Standardabweichungen über dem Mittelwert von 6 liegt. Wir hätten es zuerst umrechnen können x = 9 in eine z-Punktzahl von 0,25, aber die Software erledigt dies für uns.
Das andere ist, dass wir diese beiden Formeln wirklich nicht brauchen. NORM.S.DIST ist ein Sonderfall von NORM.DIST. Wenn der Mittelwert gleich 0 und die Standardabweichung gleich 1 ist, stimmen die Berechnungen für NORM.DIST mit denen von NORM.S.DIST überein. Beispiel: NORM.DIST (2, 0, 1, 1) = NORM.S.DIST (2, 1).
