Die Ergänzungsregel

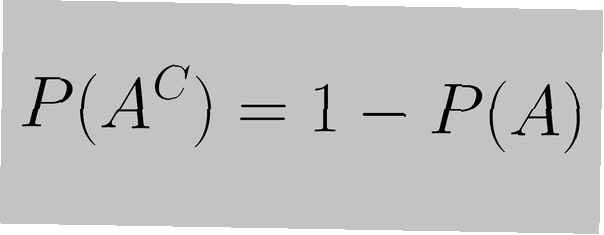
In der Statistik ist die Komplementregel ein Theorem, das einen Zusammenhang zwischen der Wahrscheinlichkeit eines Ereignisses und der Wahrscheinlichkeit des Komplements des Ereignisses auf solche Weise herstellt, dass wir, wenn wir eine dieser Wahrscheinlichkeiten kennen, automatisch die andere kennen.

Die Komplementregel ist nützlich, wenn wir bestimmte Wahrscheinlichkeiten berechnen. Oft ist die Wahrscheinlichkeit eines Ereignisses unübersichtlich oder kompliziert zu berechnen, wohingegen die Wahrscheinlichkeit seiner Ergänzung viel einfacher ist.

Bevor wir sehen, wie die Komplementregel verwendet wird, werden wir speziell definieren, was diese Regel ist. Wir beginnen mit etwas Notation. Die Ergänzung der Veranstaltung EIN, Bestehend aus allen Elementen im Probenraum S Das sind keine Elemente der Menge EIN, wird bezeichnet mit EINC.

Erklärung der Ergänzungsregel

Die Komplementregel wird angegeben als "die Summe der Wahrscheinlichkeit eines Ereignisses und der Wahrscheinlichkeit seines Komplements ist gleich 1", ausgedrückt durch die folgende Gleichung:

P (EIN^C) = 1 - P (EIN)

Das folgende Beispiel zeigt, wie die Komplementregel verwendet wird. Es wird deutlich, dass dieser Satz die Wahrscheinlichkeitsberechnung sowohl beschleunigen als auch vereinfachen wird.

Wahrscheinlichkeit ohne die Ergänzungsregel

Angenommen, wir werfen acht faire Münzen um - wie hoch ist die Wahrscheinlichkeit, dass mindestens ein Kopf angezeigt wird? Eine Möglichkeit, dies herauszufinden, besteht darin, die folgenden Wahrscheinlichkeiten zu berechnen. Der Nenner von jedem wird durch die Tatsache erklärt, dass es 2 gibt⁸ = 256 Ergebnisse, von denen jedes gleich wahrscheinlich ist. Alle folgenden uns eine Formel für Kombinationen:

• Die Wahrscheinlichkeit, genau einen Kopf umzudrehen, beträgt C (8,1) / 256 = 8/256.
• Die Wahrscheinlichkeit, genau zwei Köpfe umzudrehen, beträgt C (8,2) / 256 = 28/256.
• Die Wahrscheinlichkeit, genau drei Köpfe umzudrehen, beträgt C (8,3) / 256 = 56/256.
• Die Wahrscheinlichkeit, genau vier Köpfe umzudrehen, beträgt C (8,4) / 256 = 70/256.
• Die Wahrscheinlichkeit, genau fünf Köpfe umzudrehen, beträgt C (8,5) / 256 = 56/256.
• Die Wahrscheinlichkeit, genau sechs Köpfe umzudrehen, beträgt C (8,6) / 256 = 28/256.
• Die Wahrscheinlichkeit, genau sieben Köpfe umzudrehen, beträgt C (8,7) / 256 = 8/256.
• Die Wahrscheinlichkeit, genau acht Köpfe umzudrehen, beträgt C (8,8) / 256 = 1/256.

Da sich diese Ereignisse gegenseitig ausschließen, addieren wir die Wahrscheinlichkeiten mit einer der entsprechenden Additionsregeln. Dies bedeutet, dass die Wahrscheinlichkeit, dass wir mindestens einen Kopf haben, 255 von 256 ist.

Verwenden der Ergänzungsregel zur Vereinfachung von Wahrscheinlichkeitsproblemen

Wir berechnen nun die gleiche Wahrscheinlichkeit unter Verwendung der Komplementregel. Die Ergänzung des Ereignisses „Wir drehen mindestens einen Kopf um“ ist das Ereignis „Es gibt keine Köpfe“. Dies kann auf eine Weise geschehen, die uns die Wahrscheinlichkeit von 1/256 gibt. Wir verwenden die Komplementregel und stellen fest, dass unsere gewünschte Wahrscheinlichkeit eins minus eins von 256 ist, was 255 von 256 entspricht.

Dieses Beispiel zeigt nicht nur die Nützlichkeit, sondern auch die Kraft der Komplementregel. Obwohl an unserer ursprünglichen Berechnung nichts auszusetzen ist, war sie ziemlich aufwendig und erforderte mehrere Schritte. Im Gegensatz dazu gab es bei Verwendung der Komplementregel für dieses Problem nicht so viele Schritte, bei denen Berechnungen fehlschlagen konnten.