Kirchhoffsche Gesetze für Strom und Spannung

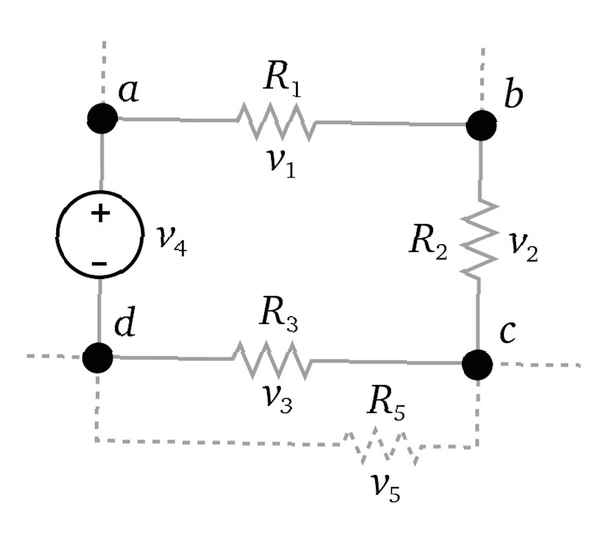
Der deutsche Physiker Gustav Kirchhoff beschrieb 1845 erstmals zwei Gesetze, die für die Elektrotechnik von zentraler Bedeutung waren. Kirchhoffs Stromgesetz, auch bekannt als Kirchhoffs Verbindungsgesetz, und Kirchhoffs Erstes Gesetz definieren die Art und Weise, wie elektrischer Strom verteilt wird, wenn er einen Verbindungspunkt durchquert - einen Punkt, an dem sich drei oder mehr Leiter treffen. Anders ausgedrückt, Kirchhoffs Gesetze besagen, dass die Summe aller Ströme, die einen Knoten in einem elektrischen Netz verlassen, immer Null ist.

Diese Gesetze sind im wirklichen Leben äußerst nützlich, da sie die Beziehung von Werten von Strömen, die durch einen Verbindungspunkt fließen, und Spannungen in einer elektrischen Stromkreisschleife beschreiben. Sie beschreiben, wie elektrischer Strom in allen Milliarden von Elektrogeräten und -geräten sowie in Haushalten und Unternehmen fließt, die ständig auf der Erde in Gebrauch sind.

Kirchhoffsche Gesetze: Die Grundlagen

Im Einzelnen heißt es in den Gesetzen:

Die algebraische Summe des Stroms in eine beliebige Verbindung ist Null.

Da es sich bei Strom um den Fluss von Elektronen durch einen Leiter handelt, kann er sich an einer Verbindungsstelle nicht aufbauen, was bedeutet, dass der Strom erhalten bleibt: Was hineingeht, muss herauskommen. Stellen Sie sich ein bekanntes Beispiel für eine Anschlussstelle vor: eine Anschlussdose. Diese Kästen werden auf den meisten Häusern angebracht. Dies sind die Kästen, in denen sich die Verkabelung befindet, durch die der gesamte Strom im Haus fließen muss.

Bei der Durchführung von Berechnungen weist der Strom, der in den Übergang hinein und aus ihm heraus fließt, typischerweise entgegengesetzte Vorzeichen auf. Sie können das geltende Kirchhoff-Gesetz auch wie folgt festlegen:

Die Summe des Stroms in einen Übergang entspricht der Summe des Stroms aus dem Übergang.

Sie können die beiden Gesetze genauer aufschlüsseln.

Kirchhoffs geltendes Gesetz

In der Abbildung ist eine Verbindung von vier Leitern (Drähten) dargestellt. Die Strömungen v₂ und v₃ fließen in die Kreuzung, während v₁ und v₄ fließe aus ihm heraus. In diesem Beispiel ergibt die Kirchhoffsche Verknüpfungsregel die folgende Gleichung:

v₂ + v₃ = v₁ + v₄

Kirchhoffs Spannungsgesetz

Das Kirchhoffsche Spannungsgesetz beschreibt die Verteilung der elektrischen Spannung innerhalb einer Schleife oder eines geschlossenen Leiterwegs eines Stromkreises. Kirchhoffs Spannungsgesetz besagt:

Die algebraische Summe der Spannungsdifferenzen (Potentialdifferenzen) in einer Schleife muss Null sein.

Die Spannungsunterschiede umfassen die mit elektromagnetischen Feldern (EMFs) und Widerstandselementen verbundenen, wie z. B. Widerstände, Stromquellen (z. B. Batterien) oder Geräte, Lampen, Fernsehgeräte und Mixer, die an den Stromkreis angeschlossen sind. Stellen Sie sich dies als steigende und fallende Spannung vor, während Sie die einzelnen Schleifen des Stromkreises umfahren.

Kirchhoffs Spannungsgesetz entsteht, weil das elektrostatische Feld in einem Stromkreis ein konservatives Kraftfeld ist. Die Spannung stellt die elektrische Energie im System dar. Stellen Sie sich diese also als konkreten Fall der Energieeinsparung vor. Wenn Sie eine Schleife umrunden und am Startpunkt ankommen, hat dies dasselbe Potenzial wie zu Beginn. Daher müssen sich alle Erhöhungen und Verringerungen entlang der Schleife für eine Gesamtänderung von Null aufheben. Andernfalls hätte das Potenzial am Start- / Endpunkt zwei unterschiedliche Werte.

Positive und negative Vorzeichen im Kirchhoffschen Spannungsgesetz

Die Verwendung der Spannungsregel erfordert einige Vorzeichenkonventionen, die nicht unbedingt so klar sind wie die in der aktuellen Regel. Wählen Sie eine Richtung (im oder gegen den Uhrzeigersinn), um die Schleife zu durchlaufen. Beim Übergang von positiv nach negativ (+ nach -) in einer EMF (Stromquelle) fällt die Spannung ab, sodass der Wert negativ ist. Beim Übergang von negativ nach positiv (- nach +) steigt die Spannung an, sodass der Wert positiv ist.

Denken Sie daran, dass Sie beim Umfahren des Stromkreises nach Kirchhoffs Spannungsgesetz immer in die gleiche Richtung (im oder gegen den Uhrzeigersinn) gehen, um festzustellen, ob ein bestimmtes Element eine Erhöhung oder Verringerung der Spannung darstellt. Wenn Sie herumspringen und sich in verschiedene Richtungen bewegen, ist Ihre Gleichung falsch.

Beim Überqueren eines Widerstands wird die Spannungsänderung durch die Formel bestimmt:

I * R

wo ich ist der Wert des aktuellen und R ist der Widerstand des Widerstands. Wenn Sie sich in der gleichen Richtung wie der Strom kreuzen, sinkt die Spannung, sodass der Wert negativ ist. Beim Überqueren eines Widerstands in die dem Strom entgegengesetzte Richtung ist der Spannungswert positiv und steigt daher an.

Anwendung des Kirchhoffschen Spannungsgesetzes

Die grundlegendsten Anwendungen der Kirchhoffschen Gesetze beziehen sich auf elektrische Schaltkreise. Sie werden sich vielleicht aus der Physik der Mittelstufe daran erinnern, dass die Elektrizität in einem Stromkreis in einer kontinuierlichen Richtung fließen muss. Wenn Sie beispielsweise einen Lichtschalter ausschalten, unterbrechen Sie den Stromkreis und schalten damit das Licht aus. Sobald Sie den Schalter erneut betätigen, schalten Sie den Stromkreis wieder ein und die Lichter gehen wieder an.

Oder denken Sie an Lichterketten an Ihrem Haus oder Weihnachtsbaum. Wenn nur eine Glühbirne ausgeht, erlischt die gesamte Lichterkette. Das liegt daran, dass der Strom, der durch das kaputte Licht gestoppt wird, keinen Platz hat, an den man gehen kann. Es ist das gleiche wie das Ausschalten des Lichtschalters und das Unterbrechen des Stromkreises. Der andere Aspekt in Bezug auf die Kirchhoffschen Gesetze ist, dass die Summe aller Ströme, die in eine Kreuzung hinein- und aus dieser herausfließen, Null sein muss. Der Strom, der in die Abzweigung fließt (und um den Stromkreis herum fließt), muss gleich Null sein, da der eingespeiste Strom auch abgegeben werden muss.

Wenn Sie also das nächste Mal an Ihrer Abzweigdose arbeiten oder einen Elektriker dabei beobachten, elektrische Weihnachtslichter zünden oder Ihren Fernseher oder Computer ein- oder ausschalten, denken Sie daran, dass Kirchhoff zuerst beschrieben hat, wie alles funktioniert, und damit das Zeitalter von eingeleitet hat Elektrizität.