Gepaarte Daten in Statistiken

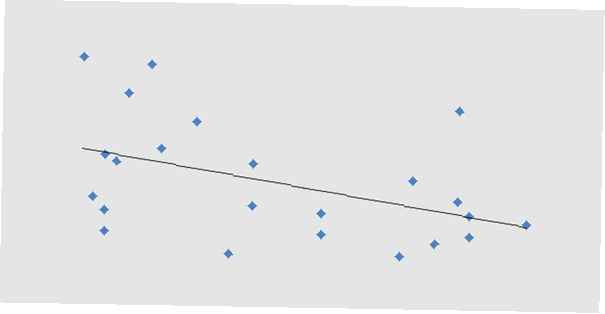
In Statistiken werden gepaarte Daten, die oft als geordnete Paare bezeichnet werden, als zwei Variablen in den Individuen einer Population bezeichnet, die miteinander verknüpft sind, um die Korrelation zwischen ihnen zu bestimmen. Damit ein Datensatz als gepaarte Daten betrachtet werden kann, müssen diese beiden Datenwerte aneinander angehängt oder miteinander verknüpft werden und dürfen nicht separat betrachtet werden.

Die Idee gepaarter Daten steht im Gegensatz zu der üblichen Zuordnung einer Zahl zu jedem Datenpunkt wie bei anderen quantitativen Datensätzen, indem jedem einzelnen Datenpunkt zwei Zahlen zugeordnet werden. Auf diese Weise erhalten Statistiker einen Graphen, mit dem sie die Beziehung zwischen diesen Variablen in beobachten können eine Bevölkerung.

Diese Methode der gepaarten Daten wird verwendet, wenn eine Studie zwei Variablen in Individuen der Population vergleichen möchte, um eine Schlussfolgerung über die beobachtete Korrelation zu ziehen. Bei der Beobachtung dieser Datenpunkte ist die Reihenfolge der Paarung wichtig, da die erste Zahl ein Maß für eine Sache ist, während die zweite ein Maß für etwas ganz anderes ist.

Beispiel für gepaarte Daten

Angenommen, ein Lehrer zählt die Anzahl der Hausaufgaben, die jeder Schüler für eine bestimmte Einheit abgegeben hat, und verbindet diese Anzahl dann mit dem Prozentsatz der Schüler beim Einheitentest. Die Paare sind wie folgt:

• Eine Person, die 10 Aufgaben erledigt hat, hat bei ihrem Test 95% verdient. (10, 95%)
• Eine Person, die 5 Aufgaben erfüllt hat, erhielt 80% ihres Tests. (5, 80%)
• Eine Person, die 9 Aufgaben erfüllt hat, verdiente 85% bei ihrem Test. (9, 85%)
• Eine Person, die zwei Aufgaben erfüllt hat, erhielt 50% für ihren Test. (2, 50%)
• Eine Person, die 5 Aufgaben erfüllt hat, erhielt 60% für ihren Test. (5, 60%)
• Eine Person, die drei Aufgaben erfüllt hat, erhielt 70% ihres Tests. (3, 70%)

In jedem dieser gepaarten Datensätze sehen wir, dass die Anzahl der Zuweisungen im geordneten Paar immer an erster Stelle steht, während der Prozentsatz, der im Test verdient wurde, an zweiter Stelle steht, wie in der ersten Instanz von (10, 95%)..

Während eine statistische Analyse dieser Daten auch zur Berechnung der durchschnittlichen Anzahl abgeschlossener Hausaufgaben oder der durchschnittlichen Testergebnisse verwendet werden kann, müssen möglicherweise andere Fragen zu den Daten gestellt werden. In diesem Fall möchte der Lehrer wissen, ob ein Zusammenhang zwischen der Anzahl der abgegebenen Hausaufgaben und der Leistung des Tests besteht, und der Lehrer muss die Daten gepaart lassen, um diese Frage zu beantworten.

Analyse gepaarter Daten

Die statistischen Techniken der Korrelation und Regression werden verwendet, um gepaarte Daten zu analysieren, wobei der Korrelationskoeffizient quantifiziert, wie eng die Daten entlang einer geraden Linie liegen, und die Stärke der linearen Beziehung misst.

Regression hingegen wird für verschiedene Anwendungen verwendet, einschließlich der Bestimmung, welche Zeile am besten zu unserem Datensatz passt. Diese Linie kann dann wiederum zum Schätzen oder Vorhersagen verwendet werden y Werte für Werte von x das war nicht Teil unseres ursprünglichen Datensatzes.

Es gibt einen speziellen Diagrammtyp, der besonders gut für gepaarte Daten geeignet ist und als Streudiagramm bezeichnet wird. In diesem Diagrammtyp repräsentiert eine Koordinatenachse eine Menge der gepaarten Daten, während die andere Koordinatenachse die andere Menge der gepaarten Daten repräsentiert.

Bei einem Streudiagramm für die obigen Daten würde die x-Achse die Anzahl der zugewiesenen Zuordnungen angeben, während die y-Achse die Punktzahlen beim Einheitentest angibt.