Positive Steigung

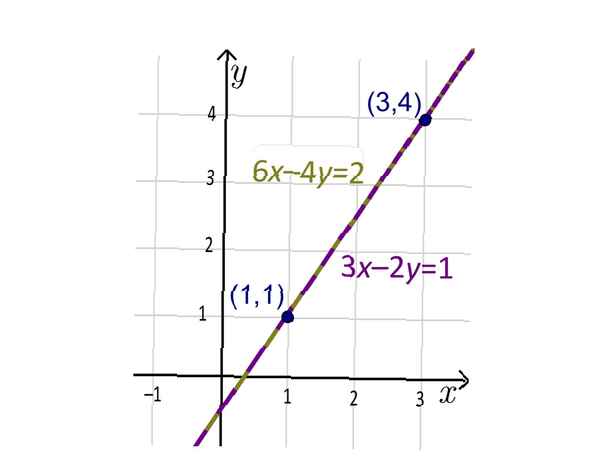
In algebraischen Funktionen wird die Steigung oder m, einer Zeile beschreibt, wie schnell oder langsam eine Änderung auftritt.

Lineare Funktionen haben 4 Arten von Steigungen: positiv, negativ, null und undefiniert.

Positive Steigung = Positive Korrelation

Eine positive Steigung zeigt eine positive Korrelation zwischen Folgendem:

• x und y
• Eingabe und Ausgabe
• unabhängige Variable und abhängige Variable
• Ursache und Wirkung

Positive Korrelation tritt auf, wenn sich jede Variable in der Funktion in die gleiche Richtung bewegt. Sehen Sie sich die lineare Funktion im Bild Positive Steigung an, m > 0. Als die Werte von x erhöhen, ansteigen, die Werte von y erhöhen, ansteigen. Ziehen Sie die Linie mit Ihrem Finger von links nach rechts. Beachten Sie, dass die Linie erhöht sich.

Als nächstes ziehen Sie die Linie mit Ihrem Finger von rechts nach links. Als die Werte von x verringern, die Werte von y verringern. Beachten Sie, wie die Linie nimmt ab.

Positive Steigung in der realen Welt

Hier einige Beispiele für Situationen in der realen Welt, in denen eine positive Korrelation auftreten kann:

• Samantha plant ein Familientreffen. Je mehr Personen teilnehmen (Eingang), je mehr Stühle sie bestellt (Ausgabe).
• James besucht die Bahamas. Je weniger Zeit er schnorchelt (Eingang), je weniger tropische Fische er ausspioniert (Ausgabe).

Berechnung der positiven Steigung

Es gibt mehrere Möglichkeiten, eine positive Steigung zu berechnen m> 0. Erfahren Sie, wie Sie die Steigung einer Linie mithilfe eines Diagramms ermitteln und die Steigung mithilfe einer Formel berechnen.