Die assoziativen und kommutativen Eigenschaften

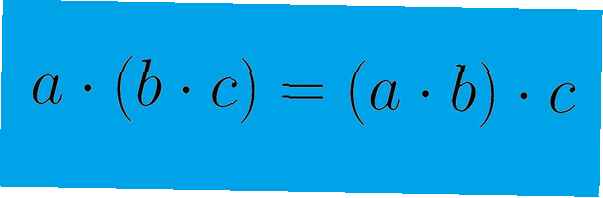
Es gibt verschiedene mathematische Eigenschaften, die in Statistiken und Wahrscheinlichkeiten verwendet werden. Zwei davon, die kommutativen und assoziativen Eigenschaften, sind im Allgemeinen mit der Grundrechenart von ganzen Zahlen, Rationalen und reellen Zahlen verbunden, obwohl sie auch in der fortgeschritteneren Mathematik auftauchen.

Diese Eigenschaften - Kommutativ und Assoziativ - sind sehr ähnlich und können leicht verwechselt werden. Aus diesem Grund ist es wichtig, den Unterschied zwischen den beiden zu verstehen.

Die kommutative Eigenschaft betrifft die Reihenfolge bestimmter mathematischer Operationen. Für eine binäre Operation - eine, die nur zwei Elemente umfasst - kann dies durch die Gleichung a + b = b + a gezeigt werden. Die Operation ist kommutativ, da die Reihenfolge der Elemente das Ergebnis der Operation nicht beeinflusst. Die assoziative Eigenschaft betrifft dagegen die Gruppierung von Elementen in einer Operation. Dies kann durch die Gleichung (a + b) + c = a + (b + c) gezeigt werden. Die in Klammern angegebene Gruppierung der Elemente hat keinen Einfluss auf das Ergebnis der Gleichung. Beachten Sie, dass Elemente in einer Gleichung verwendet werden, wenn die kommutative Eigenschaft verwendet wird neu angeordnet. Bei Verwendung der assoziativen Eigenschaft handelt es sich lediglich um Elemente umgruppiert.

Kommutativgesetz

Einfach ausgedrückt, die kommutative Eigenschaft besagt, dass die Faktoren in einer Gleichung frei angeordnet werden können, ohne das Ergebnis der Gleichung zu beeinflussen. Die kommutative Eigenschaft befasst sich daher mit der Reihenfolge von Operationen, einschließlich der Addition und Multiplikation von reellen Zahlen, ganzen Zahlen und rationalen Zahlen.

Zum Beispiel können die Zahlen 2, 3 und 5 in beliebiger Reihenfolge addiert werden, ohne das Endergebnis zu beeinflussen:

2 + 3 + 5 = 10

3 + 2 + 5 = 10

5 + 3 + 2 = 10

Die Zahlen können ebenfalls in beliebiger Reihenfolge multipliziert werden, ohne das Endergebnis zu beeinflussen:

2 x 3 x 5 = 30

3 x 2 x 5 = 30

5 x 3 x 2 = 30

Subtraktion und Division sind jedoch keine Operationen, die kommutativ sein können, da die Reihenfolge der Operationen wichtig ist. Die drei Zahlen oben kann nicht, Beispielsweise kann in beliebiger Reihenfolge subtrahiert werden, ohne den Endwert zu beeinflussen:

2 - 3 - 5 = -6

3 - 5 - 2 = -4

5 - 3 - 2 = 0