Die Nummer Pi 3.14159265…

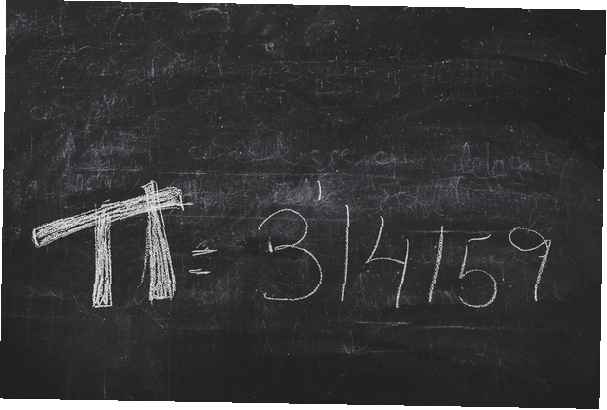
Eine der in der Mathematik am häufigsten verwendeten Konstanten ist die Zahl pi, die mit dem griechischen Buchstaben π bezeichnet wird. Das Konzept von pi hat seinen Ursprung in der Geometrie, aber diese Zahl hat Anwendungen in der gesamten Mathematik und zeigt sich in weitreichenden Fächern, einschließlich Statistik und Wahrscheinlichkeit. Pi hat sogar kulturelle Anerkennung und seinen eigenen Urlaub erlangt, mit der Feier von Pi Day-Aktivitäten auf der ganzen Welt.

Der Wert von Pi

Pi ist definiert als das Verhältnis des Umfangs eines Kreises zu seinem Durchmesser. Der Wert von pi ist etwas größer als drei, was bedeutet, dass jeder Kreis im Universum einen Umfang mit einer Länge hat, die etwas mehr als das Dreifache seines Durchmessers beträgt. Genauer gesagt hat pi eine Dezimaldarstellung, die mit 3.14159265 beginnt. Dies ist nur ein Teil der Dezimalerweiterung von pi.

Pi Fakten

Pi hat viele faszinierende und ungewöhnliche Eigenschaften, darunter: 

• Pi ist eine irrationale reelle Zahl. Dies bedeutet, dass pi nicht als Bruch ausgedrückt werden kann a / b wo ein und b sind beide ganze Zahlen. Obwohl die Zahlen 22/7 und 355/113 bei der Schätzung von pi hilfreich sind, ist keine dieser Brüche der wahre Wert von pi.
• Da pi eine irrationale Zahl ist, wird ihre Dezimalerweiterung niemals beendet oder wiederholt. Zu dieser Dezimalerweiterung gibt es einige Fragen, z. B .: Erscheint jede mögliche Ziffernfolge irgendwo in der Dezimalerweiterung von pi? Wenn jede mögliche Zeichenfolge angezeigt wird, befindet sich Ihre Handynummer irgendwo in der Erweiterung von pi (aber alle anderen auch)..
• Pi ist eine transzendentale Zahl. Dies bedeutet, dass pi nicht die Null eines Polynoms mit ganzzahligen Koeffizienten ist. Diese Tatsache ist wichtig, wenn Sie erweiterte Funktionen von pi untersuchen.
• Pi ist geometrisch wichtig und nicht nur, weil es den Umfang und den Durchmesser eines Kreises in Beziehung setzt. Diese Zahl erscheint auch in der Formel für die Fläche eines Kreises. Die Fläche eines Radiuskreises r ist EIN = pi r². Die Zahl pi wird in anderen geometrischen Formeln verwendet, wie z. B. der Oberfläche und dem Volumen einer Kugel, dem Volumen eines Kegels und dem Volumen eines Zylinders mit kreisförmiger Basis.
• Pi erscheint, wenn es am wenigsten erwartet wird. Betrachten Sie für eines von vielen Beispielen die unendliche Summe 1 + 1/4 + 1/9 + 1/16 + 1/25 + ... Diese Summe konvergiert gegen den Wert pi²/ 6.

Pi in Statistik und Wahrscheinlichkeit

Pi taucht in der gesamten Mathematik überraschend auf, und einige dieser Erscheinungen sind Gegenstand von Wahrscheinlichkeiten und Statistiken. Die Formel für die Standardnormalverteilung, auch Glockenkurve genannt, bezeichnet die Zahl pi als Normierungskonstante. Mit anderen Worten, wenn Sie durch einen Ausdruck mit pi dividieren, können Sie sagen, dass die Fläche unter der Kurve gleich eins ist. Pi ist auch Teil der Formeln für andere Wahrscheinlichkeitsverteilungen.

Ein weiteres überraschendes Auftreten von pi in der Wahrscheinlichkeit ist ein jahrhundertealtes Nadelwurfexperiment. Im 18. Jahrhundert stellte Georges-Louis Leclerc von Comte de Buffon die Frage nach der Wahrscheinlichkeit, Nadeln fallen zu lassen: Beginnen Sie mit einem Boden aus Holzbrettern mit gleichmäßiger Breite, bei dem die Linien zwischen den einzelnen Brettern parallel zueinander verlaufen. Nehmen Sie eine Nadel mit einer Länge, die kürzer als der Abstand zwischen den Planken ist. Wenn Sie eine Nadel auf den Boden fallen lassen, wie hoch ist die Wahrscheinlichkeit, dass sie auf einer Linie zwischen zwei Holzbrettern landet??

Wie sich herausstellt, ist die Wahrscheinlichkeit, dass die Nadel auf einer Linie zwischen zwei Planken landet, doppelt so groß wie die Länge der Nadel geteilt durch die Länge zwischen den Planken mal pi.