Arbeitsblatt für Chebyshevs Ungleichung

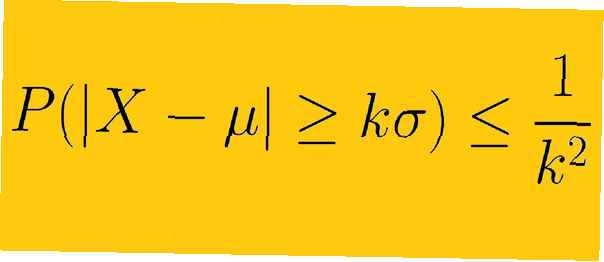
Chebyshevs Ungleichung besagt, dass mindestens 1 -1 /K² von Daten aus einer Stichprobe muss innerhalb liegen K Standardabweichungen vom Mittelwert, wo K ist eine positive reelle Zahl größer als eins. Dies bedeutet, dass wir die Form der Verteilung unserer Daten nicht kennen müssen. Mit nur dem Mittelwert und der Standardabweichung können wir die Datenmenge einer bestimmten Anzahl von Standardabweichungen vom Mittelwert bestimmen.

Das Folgende sind einige Probleme beim Üben mit der Ungleichung.

Beispiel 1

Eine Klasse von Zweitklässlern hat eine durchschnittliche Höhe von fünf Fuß mit einer Standardabweichung von einem Zoll. Mindestens wie viel Prozent der Klasse müssen zwischen 4'10 "und 5'2" sein?

Lösung

Die im obigen Bereich angegebenen Höhen liegen innerhalb von zwei Standardabweichungen von der mittleren Höhe von fünf Fuß. Chebyshevs Ungleichung besagt, dass mindestens 1 - 1/2² = 3/4 = 75% der Klasse liegt im angegebenen Höhenbereich.

Beispiel # 2

Computer eines bestimmten Unternehmens halten im Durchschnitt drei Jahre ohne Hardwarefehler mit einer Standardabweichung von zwei Monaten. Zumindest wie viel Prozent der Computer zwischen 31 und 41 Monaten halten?

Lösung

Die mittlere Lebensdauer von drei Jahren entspricht 36 Monaten. Die Zeiten von 31 Monaten bis 41 Monaten betragen jeweils 5/2 = 2,5 Standardabweichungen vom Mittelwert. Nach Chebyshevs Ungleichung mindestens 1 - 1 / (2.5) 6² = 84% der Computer halten zwischen 31 und 41 Monaten.

Beispiel # 3

Bakterien in einer Kultur leben durchschnittlich drei Stunden mit einer Standardabweichung von 10 Minuten. Zumindest welcher Anteil der Bakterien lebt zwischen zwei und vier Stunden?

Lösung

Zwei und vier Stunden sind jeweils eine Stunde vom Mittelwert entfernt. Eine Stunde entspricht sechs Standardabweichungen. Also mindestens 1 - 1/6² = 35/36 = 97% der Bakterien leben zwischen zwei und vier Stunden.

Beispiel # 4

Was ist die kleinste Anzahl von Standardabweichungen vom Mittelwert, den wir gehen müssen, wenn wir sicherstellen möchten, dass wir mindestens 50% der Daten einer Verteilung haben?

Lösung

Hier verwenden wir die Ungleichung von Chebyshev und arbeiten rückwärts. Wir wollen 50% = 0,50 = 1/2 = 1 - 1 /K². Das Ziel ist es, mit Algebra zu lösen K.

Wir sehen, dass 1/2 = 1 /K². Kreuzen Sie multiplizieren und sehen Sie, dass 2 =K². Wir ziehen die Quadratwurzel von beiden Seiten und von da K Ist eine Reihe von Standardabweichungen, ignorieren wir die negative Lösung der Gleichung. Dies zeigt, dass K ist gleich der Quadratwurzel von zwei. Mindestens 50% der Daten liegen also innerhalb von ca. 1,4 Standardabweichungen vom Mittelwert.

Beispiel # 5

Die Buslinie Nr. 25 benötigt durchschnittlich 50 Minuten mit einer Standardabweichung von 2 Minuten. Auf einem Werbeplakat für dieses Bussystem heißt es: „95% der Zeit, in der Buslinie Nr. 25 von ____ bis _____ Minuten fährt.“ Mit welchen Zahlen würden Sie die Leerzeichen ausfüllen??