Einführung in die Dirac Delta-Funktion

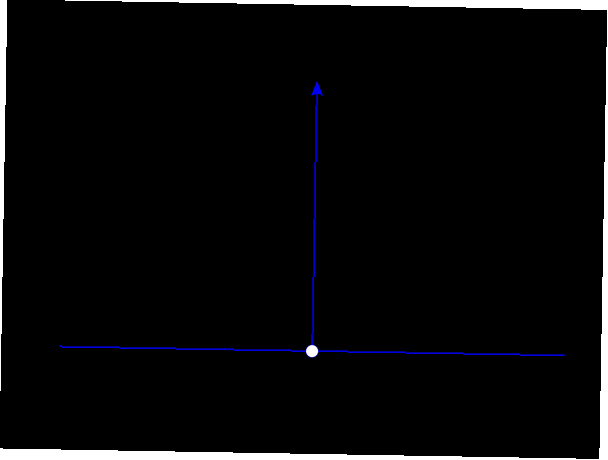
Die Dirac-Delta-Funktion ist die Bezeichnung für eine mathematische Struktur, die ein idealisiertes Punktobjekt darstellen soll, z. B. eine Punktmasse oder eine Punktladung. Es findet breite Anwendung in der Quantenmechanik und der übrigen Quantenphysik, wie es üblicherweise in der Quantenwellenfunktion verwendet wird. Die Delta-Funktion wird mit dem griechischen Kleinbuchstaben Delta dargestellt, geschrieben als Funktion: δ (x).

So funktioniert die Delta-Funktion

Diese Darstellung wird erreicht, indem die Dirac-Delta-Funktion so definiert wird, dass sie überall den Wert 0 hat, mit Ausnahme des Eingabewerts 0. Zu diesem Zeitpunkt stellt sie eine Spitze dar, die unendlich hoch ist. Das über die gesamte Linie genommene Integral ist gleich 1. Wenn Sie die Analysis studiert haben, sind Sie wahrscheinlich schon einmal auf dieses Phänomen gestoßen. Denken Sie daran, dass dies ein Konzept ist, das Studenten normalerweise nach Jahren des Studiums der theoretischen Physik auf Hochschulniveau vorgestellt wird.

Mit anderen Worten sind die Ergebnisse für die grundlegendste Delta-Funktion δ (x), mit einer eindimensionalen Variablen x, für einige zufällige Eingabewerte:

• δ (5) = 0
• δ (-20) = 0
• δ (38,4) = 0
• δ (-12,2) = 0
• δ (0,11) = 0
• δ (0) = ∞

Sie können die Funktion vergrößern, indem Sie sie mit einer Konstanten multiplizieren. Nach den Regeln der Analysis erhöht die Multiplikation mit einem konstanten Wert auch den Wert des Integrals um diesen konstanten Faktor. Da das Integral von δ (x) über alle reellen Zahlen ist 1, dann würde das Multiplizieren mit einer Konstanten von ein neues Integral haben, das dieser Konstante entspricht. So zum Beispiel 27δ (x) hat ein Integral über alle reellen Zahlen von 27.

Da die Funktion nur für die Eingabe von 0 einen Wert ungleich Null hat, können Sie ein Koordinatengitter verwenden, bei dem Ihr Punkt nicht genau auf 0 ausgerichtet ist Ein Ausdruck innerhalb der Funktionseingabe. Wenn Sie also die Idee darstellen möchten, dass sich das Partikel an einer Position befindet x = 5, dann schreiben Sie die Dirac-Delta-Funktion als δ (x - 5) = ∞ [da δ (5 - 5) = ∞]. 

Wenn Sie diese Funktion dann verwenden möchten, um eine Reihe von Punktpartikeln innerhalb eines Quantensystems darzustellen, können Sie dies tun, indem Sie verschiedene Dirac-Delta-Funktionen addieren. Für ein konkretes Beispiel könnte eine Funktion mit Punkten bei x = 5 und x = 8 als δ (x - 5) + δ (x - 8) dargestellt werden. Wenn Sie dann ein Integral dieser Funktion über alle Zahlen nehmen, erhalten Sie ein Integral, das reelle Zahlen darstellt, obwohl die Funktionen an allen anderen Stellen als den beiden Stellen, an denen Punkte vorhanden sind, 0 sind. Dieses Konzept kann dann erweitert werden, um einen Raum mit zwei oder drei Dimensionen darzustellen (anstelle des eindimensionalen Falls, den ich in meinen Beispielen verwendet habe)..

Dies ist eine zugegebenermaßen kurze Einführung in ein sehr komplexes Thema. Entscheidend dabei ist, dass die Dirac-Delta-Funktion im Wesentlichen nur dazu dient, die Integration der Funktion sinnvoll zu gestalten. Wenn kein Integral stattfindet, ist das Vorhandensein der Dirac-Delta-Funktion nicht besonders hilfreich. Aber in der Physik ist es sehr hilfreich, wenn Sie von einer Region ausgehen, in der es keine Partikel gibt, die plötzlich nur an einem Punkt existieren.

Quelle der Delta-Funktion

In seinem 1930er Buch, Prinzipien der Quantenmechanik, Der englische theoretische Physiker Paul Dirac legte die Schlüsselelemente der Quantenmechanik dar, einschließlich der Bracket-Notation und seiner Dirac-Delta-Funktion. Diese wurden zu Standardkonzepten auf dem Gebiet der Quantenmechanik innerhalb der Schrödinger-Gleichung.