Formelverknüpfung für Quadratsumme
 Share
Share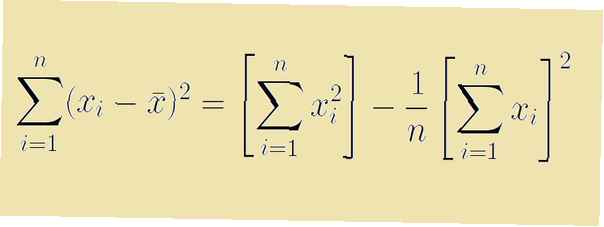
Die Berechnung einer Stichprobenvarianz oder Standardabweichung wird typischerweise als Bruch angegeben. Der Zähler dieses Bruchs enthält eine Summe der quadratischen Abweichungen vom Mittelwert. In der Statistik lautet die Formel für diese Gesamtsumme der Quadrate
Σ (xich - x̄)2
Hier bezieht sich das Symbol x̄ auf den Stichprobenmittelwert, und das Symbol Σ weist uns an, die quadratischen Differenzen (xich - x̄) für alle ich.
Während diese Formel für Berechnungen verwendet werden kann, gibt es eine entsprechende Abkürzungsformel, bei der wir nicht zuerst den Stichprobenmittelwert berechnen müssen. Diese Abkürzungsformel für die Summe der Quadrate lautet
Σ (xich2) - (Σ xich)2/n
Hier die Variable n bezieht sich auf die Anzahl der Datenpunkte in unserer Stichprobe.
Standardformel Beispiel
Um zu sehen, wie diese Verknüpfungsformel funktioniert, betrachten wir ein Beispiel, das mit beiden Formeln berechnet wird. Angenommen, unsere Stichprobe ist 2, 4, 6, 8. Der Stichprobenmittelwert ist (2 + 4 + 6 + 8) / 4 = 20/4 = 5. Nun berechnen wir die Differenz jedes Datenpunkts mit dem Mittelwert 5.
- 2 - 5 = -3
- 4 - 5 = -1
- 6 - 5 = 1
- 8 - 5 = 3
Wir quadrieren nun jede dieser Zahlen und addieren sie. (-3)2 + (-1)2 + 12 + 32 = 9 + 1 + 1 + 9 = 20.
Beispiel für eine Verknüpfungsformel
Jetzt verwenden wir denselben Datensatz: 2, 4, 6, 8 mit der Verknüpfungsformel, um die Summe der Quadrate zu bestimmen. Wir quadrieren zuerst jeden Datenpunkt und addieren sie: 22 + 42 + 62 + 82 = 4 + 16 + 36 + 64 = 120.
Der nächste Schritt besteht darin, alle Daten zu addieren und diese Summe zu quadrieren: (2 + 4 + 6 + 8)2 = 400. Wir dividieren dies durch die Anzahl der Datenpunkte, um 400/4 = 100 zu erhalten.
Wir subtrahieren diese Zahl jetzt von 120. Dies gibt uns die Summe der quadratischen Abweichungen von 20. Dies war genau die Zahl, die wir bereits aus der anderen Formel herausgefunden haben.
Wie funktioniert das?
Viele Leute akzeptieren die Formel zum Nennwert und haben keine Ahnung, warum diese Formel funktioniert. Mit ein wenig Algebra können wir sehen, warum diese Abkürzungsformel der herkömmlichen Methode zur Berechnung der Summe der quadratischen Abweichungen entspricht.
Obwohl ein realer Datensatz Hunderte, wenn nicht Tausende von Werten enthält, gehen wir davon aus, dass es nur drei Datenwerte gibt: x1 , x2, x3. Was wir hier sehen, könnte auf einen Datensatz mit Tausenden von Punkten erweitert werden.
Wir beginnen damit, dass (x1 + x2 + x3) = 3 x & spplus ;. Der Ausdruck Σ (xich - x̄)2 = (x1 - x̄)2 + (x2 - x̄)2 + (x3 - x̄)2.
