Was sind Wahrscheinlichkeitsaxiome?

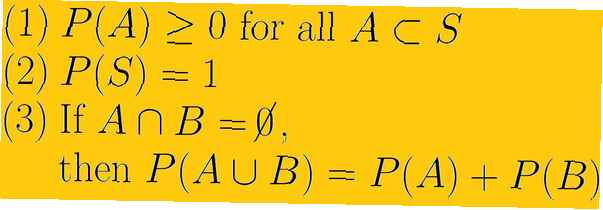
Eine Strategie in der Mathematik besteht darin, mit ein paar Aussagen zu beginnen und dann mehr Mathematik aus diesen Aussagen aufzubauen. Die Anfangsaussagen werden als Axiome bezeichnet. Ein Axiom ist typischerweise etwas, das mathematisch selbstverständlich ist. Aus einer relativ kurzen Liste von Axiomen wird deduktive Logik verwendet, um andere Aussagen zu beweisen, die Theoreme oder Sätze genannt werden.

Das Gebiet der Mathematik, bekannt als Wahrscheinlichkeit, ist nicht anders. Die Wahrscheinlichkeit kann auf drei Axiome reduziert werden. Dies wurde zuerst vom Mathematiker Andrei Kolmogorov gemacht. Die wenigen Axiome, die der Wahrscheinlichkeit zugrunde liegen, können verwendet werden, um alle möglichen Ergebnisse abzuleiten. Aber was sind diese Wahrscheinlichkeitsaxiome??

Definitionen und Vorbemerkungen

Um die Axiome für die Wahrscheinlichkeit zu verstehen, müssen wir zunächst einige grundlegende Definitionen diskutieren. Wir nehmen an, dass wir eine Reihe von Ergebnissen haben, die als Probenraum bezeichnet werden S. Dieser Probenraum kann als universeller Satz für die Situation angesehen werden, die wir untersuchen. Der Sampleraum besteht aus Teilmengen, die als Ereignisse bezeichnet werden E₁, E₂,… , E_n. 

Wir gehen auch davon aus, dass es eine Möglichkeit gibt, einem Ereignis eine Wahrscheinlichkeit zuzuweisen E. Dies kann als eine Funktion betrachtet werden, die eine Menge für eine Eingabe und eine reelle Zahl als eine Ausgabe hat. Die Wahrscheinlichkeit des Ereignisses E wird bezeichnet mit P(E).

Axiom One

Das erste Axiom der Wahrscheinlichkeit ist, dass die Wahrscheinlichkeit eines Ereignisses eine nicht negative reelle Zahl ist. Dies bedeutet, dass die kleinste Wahrscheinlichkeit, die eine Wahrscheinlichkeit jemals sein kann, Null ist und dass sie nicht unendlich sein kann. Die Menge der Zahlen, die wir verwenden können, sind reelle Zahlen. Dies bezieht sich sowohl auf rationale Zahlen, die auch als Brüche bezeichnet werden, als auch auf irrationale Zahlen, die nicht als Brüche geschrieben werden können.

Zu beachten ist, dass dieses Axiom nichts darüber aussagt, wie groß die Wahrscheinlichkeit eines Ereignisses sein kann. Das Axiom eliminiert die Möglichkeit negativer Wahrscheinlichkeiten. Es spiegelt die Vorstellung wider, dass die kleinste Wahrscheinlichkeit, die für unmögliche Ereignisse reserviert ist, Null ist.

Axiom Zwei

Das zweite Axiom der Wahrscheinlichkeit ist, dass die Wahrscheinlichkeit des gesamten Probenraums eins ist. Symbolisch schreiben wir P(S) = 1. In diesem Axiom ist die Vorstellung impliziert, dass der Probenraum für unser Wahrscheinlichkeitsexperiment alles Mögliche ist und dass es keine Ereignisse außerhalb des Probenraums gibt.

Dieses Axiom setzt für sich genommen keine Obergrenze für die Wahrscheinlichkeiten von Ereignissen, bei denen es sich nicht um den gesamten Probenraum handelt. Es spiegelt wider, dass etwas mit absoluter Sicherheit eine Wahrscheinlichkeit von 100% hat.

Axiom Drei

Das dritte Wahrscheinlichkeitsaxiom befasst sich mit sich gegenseitig ausschließenden Ereignissen. Wenn E₁ und E₂ schließen sich gegenseitig aus, was bedeutet, dass sie eine leere Kreuzung haben und wir dann U verwenden, um die Vereinigung zu bezeichnen P(E₁ U E₂ ) = P(E₁) + P(E₂).

Das Axiom deckt die Situation tatsächlich mit mehreren (sogar unendlich vielen) Ereignissen ab, von denen sich jedes Paar gegenseitig ausschließt. Solange dies eintritt, ist die Wahrscheinlichkeit der Vereinigung der Ereignisse dieselbe wie die Summe der Wahrscheinlichkeiten:

P(E₁ U E₂ U… U E_n ) = P(E₁) + P(E₂) +… + E_n

Obwohl dieses dritte Axiom vielleicht nicht so nützlich erscheint, werden wir sehen, dass es in Kombination mit den anderen beiden Axiomen in der Tat ziemlich mächtig ist.

Axiom-Anwendungen

Die drei Axiome setzen eine Obergrenze für die Wahrscheinlichkeit eines Ereignisses. Wir bezeichnen die Ergänzung der Veranstaltung E durch E^C. Aus der Mengenlehre, E und E^C haben eine leere Kreuzung und schließen sich gegenseitig aus. Außerdem E U E^C = S, der gesamte Probenraum.

Diese Tatsachen ergeben zusammen mit den Axiomen: